LCA-RMQ-ST 模板

LCA分为在线算法和离线算法，这里介绍的是在线算法中的ST算法。

LCA定义

最近公共祖先是指在一个树或者有向无环图中同时拥有V和W作为后代的最深的结点。
在这里，我们定义一个节点也是其自己的后代，因此如果v是ｗ的后代，那么ｗ就是ｖ和ｗ的
最近公共祖先。

LCA->RMQ

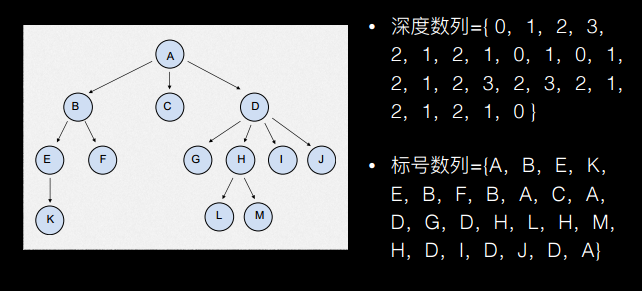
DFS，每经过一个点，就记录下这个点的深度和标号
如此得到两个数组：深度数组和标号数组，元素均为2*n-1个。
对于标号数组中的任何两个点，他们的下标在深度数组中对应一个区间，这个区间的最小值就对应着这两个点的LCA。

RMQ–ST–预处理

全称：Sparse Table算法
dp[i][j]表示区间[j,j+2^i-1]的最小值

1 2	dp[0][j]=a[j] dp[i][j]=min{dp[i-1][j],dp[i-1][j+2^(i-1)]}

时间复杂度：O(nlogn)

一些理解

现在问题转化为求一个区间最小值，普通算法就是直接遍历区间，即可找到最值。数据量较大时，RMQ是一种
更高效的算法。通过预处理，我们得到的dp数组储存了这个大区间中任意起点任意长度（其实长度是2的N次方，但可以这么理解算法）的小区间的最小值。
之所以高效就高效在预处理上，通过旧区间的最值得到更大区间的最值，从前到后，就短到长，即可得到所有
区间的最小值。

RMQ–ST–查询

查询区间：[s,t]

1 2	k=(int)log2(t-s+1) RMQ[s,t]=min{dp[k][s],dp[k][t-(1<<k)+1]}

时间复杂度：O(1)

一些理解

查询的话只需要将已知区间转化为dp数组的格式，如果长度不符合2的N次方的形式，就把大区间
变成两个符合形式的一前一后区间，直接比较这两个区间的最值即可得到想查询的区间的最值。

附加代码

定义

#define maxn 100005
struct node
{
        int x;
};
vector<node> V[maxn]; //储存树的结构，也可以使用邻接表
int E[maxn * 2], D[maxn * 2], first[maxn]; //标号数列   深度数列   某个标号第一次出现的位置
int vis[maxn], dis[maxn], n, m, top = 1, root[maxn], st; //dis[] 若边有权值可求距离   root[] 求整棵树的根
int dp[30][maxn * 2];  //储存某区间最小值的下标

算法函数

void dfs(int u, int dep)
{
        vis[u] = 1, E[top] = u, D[top] = dep, first[u] = top++;
        for (int i = 0; i < V[u].size(); i++)
                if (!vis[V[u][i].x]) //储存时双向，因此判断是否为父节点
                {
                        int v = V[u][i].x;
                        dfs(v, dep + 1);
                        E[top] = u, D[top++] = dep; //dfs回溯过程必须储存，否则原理就错误了
                }
}
void ST(int num)
{
        for (int i = 1; i <= num; i++)//初始状态
        {
                dp[0][i] = i;
        }
        for (int i = 1; i <= log2(num); i++) //控制区间长度
                for (int j = 1; j <= num; j++) //控制区间左端点
                        if (j + (1 << i) - 1 <= num)
                        {
                                int a = dp[i - 1][j], b = dp[i - 1][j + (1 << i >> 1)];
                                if (D[a] < D[b]) //储存D数组下标，以便找到对应的E数组
                                {
                                        dp[i][j] = a; 
                                }
                                else
                                {
                                        dp[i][j] = b;
                                }
                        }
}
int RMQ(int x, int y)
{
        int k = (int) log2(y - x + 1.0);
        int a = dp[k][x], b = dp[k][y - (1 << k) + 1];
        if (D[a] < D[b]) //前后两段比较
        {
                return a;
        }
        return b;
}