Tarjan离线算法 模板

本文介绍的是LCA算法中的tarjan离线算法。

---

不知道LCA定义？请戳这儿

---

核心思想

• 并查集

pre[u]表示u点的父亲
pre[pre[pre[…u…]]]可以求u的某一层父亲结点

• 原理

tanjan离线算法的实现并不好叙述，需要深刻理解DFS的过程。给定一棵树，如下：

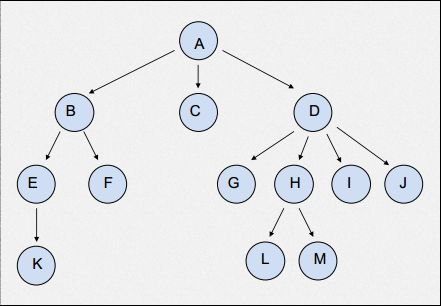
如果我们想求K与F的最近公共祖先，我们先把K和F连接，K指向F，F同样指向K。在DFS过程中，
首先从根节点A开始遍历，然后假设遍历到B，再从B开始遍历，到E，到K，然后返回，用一个数组
记录K点已经完全遍历，并在回溯的过程中建立并查集，即：

vis[K]=1
pre[K]=E

再返回

vis[E]=1
pre[E]=B

然后遍历的F，发现F的连接点K已经完全遍历，则寻找K此时的父节点，找到B点，则B为K、E的LCA。

总结

将所有想要寻找的点对连接起来，若某一点的连接点已经完全遍历，对其连接点找此时树的根，
由于树（并查集）是在DFS回溯过程中建立的，此时这个小树的根即为这两点的LCA。时间复杂度：O(n+q)

附加代码

定义及初始化

#define maxn 10005
int pre[maxn], point[maxn], point2[maxn];
// 储存树  树的邻接表数组  要查询的边的邻接表数组
bool vis[maxn];
//是否完全遍历
struct Edge
{
        int v; //连接点
        int next; //下一条从此边的出发点发出的边的序号
} edge[maxn * 2]; //邻接表   跟邻接矩阵一样，就是一种表示连接关系的结构
struct Query
{
        int v;
        int w; //找到后LCA后用来储存LCA的
        int next;
} query[maxn]; //要查询的边的邻接表
int top, top2; //两邻接表的下标变量
int init()
{
        memset(vis, 0, sizeof(vis));
        memset(point, -1, sizeof(point)); //邻接表数组初始化，一般都初始化为-1
        memset(point2, -1, sizeof(point2));
        top = 0;
        top2 = 0;
}

算法函数

int add_edge(int u, int v) //加边函数，单向的
{
        edge[top].v = v;
        edge[top].next = point[u]; ///上一条边的编号
        point[u] = top++; //更新 储存该点刚才所连接的边的编号
}
int add_query(int u, int v) //要查询的边的加边函数，双向的
{
        query[top2].v = v;
        query[top2].w = -1;
        query[top2].next = point2[u];
        point2[u] = top2++;
        query[top2].v = u;
        query[top2].w = -1;
        query[top2].next = point2[v];
        point2[v] = top2++;
}
int findset(int x) ///并查集
{
        if (x != pre[x])
        {
                pre[x] = findset(pre[x]); //路径压缩
        }
        return pre[x];
}
int lca(int u, int f) ///当前节点，父节点
{
        pre[u] = u; ///设立当前节点的集合 表示该点是树的根
        for (int i = point[u]; i != -1; i = edge[i].next)
        {
                if (edge[i].v == f)
                {
                        continue;
                }
                lca(edge[i].v, u); ///搜索子树
                pre[edge[i].v] = u; ///合并子树
        }
        vis[u] = 1; ///以u点为集合的点搜索完毕
        for (int i = point2[u]; i != -1; i = query[i].next)
        {
                if (vis[query[i].v] == 1)
                {
                        query[i].w = findset(query[i].v); //储存LCA
                }
        }
        return 0;
}